양자역학은 복잡해야 하는가?

“(Must Quantum Mechanics be complex?)

In quantum mechanics we use complex numbers and the wavefunction is itself also complex-valued. Any complex number z can be written in terms of real numbers as z= x+i y, with two real variables x and y and i²= -1.

The sums and the products of such numbers are also complex numbers, so you can make an algebra of complex numbers in the same way as the algebra of real numbers, but complex numbers are ‘much bigger and can do more’. The real numbers are basically the numbers on a line, they are 1-dimensional, but each complex number z can be drawn in a 2-dimensional plane, e.g. with x, the real part, horizontally and y, the imaginary part, on a vertical line.

Multiplication in this plane has a meaning, which goes further than the meaning of multiplication of real numbers: multiply by the imaginary number i does a rotation of 90 degree to the left in this plane. Indeed, the number i itself on the vertical axis is the real number 1 on the real axis rotated over 90 degrees. So complex numbers are useful when dealing with rotations and periodic functions. A famous identity says that

exp(i φ) = cos(φ)+ i sin(φ) [Euler-identity]

so you can use exp(i φ) to simultaneously describe cosine and sine waves.

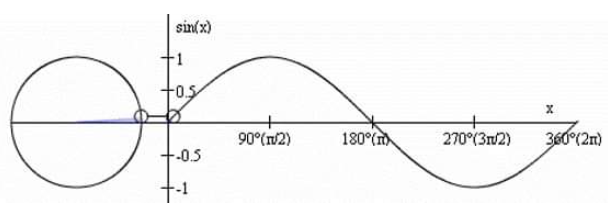
Below is an example (if the gif-value shows up moving) how a rotating point z=exp(i ωt) with frequency ω produces in time a cosine x=cos(ωt) on the real axis.

The derivative of this exponential function is i.exp(i φ) and contains the function itself again, very handy, whereas the derivatives of a cosine flips to a sine and vice versa, very annoying…

The question is: can we also use real-valued-quantum mechanics?

​

“(양자역학은 복잡해야 하는가?)

양자역학에서는 복소수를 사용하며 파동함수 자체도 복소수 값을 갖습니다. 모든 복소수 z는 두 개의 실수 변수 x와 y 및 i²= -1을 사용하여 z= x+i y와 같이 실수로 표현될 수 있습니다.

​

그러한 숫자의 합과 곱도 복소수이므로 실수의 대수와 같은 방법으로 복소수의 대수를 만들 수 있지만, 복소수는 ‘훨씬 더 크고 더 많은 일을 할 수 있다’. 실수는 기본적으로 선 위의 숫자이며 1차원이지만 각 복소수 z는 2차원 평면에 그릴 수 있습니다. x는 실수 부분을 수평으로, y는 허수 부분을 수직 라인에 배치합니다.

​

이 평면에서의 곱셈은 실수 곱셈의 의미보다 더 나아가 의미를 갖습니다. 허수 i를 곱하면 이 평면에서 왼쪽으로 90도 회전합니다. 실제로 세로축의 숫자 i 자체는 90도 이상 회전한 실제 축의 실수 1입니다. 따라서 복소수는 회전과 주기 함수를 다룰 때 유용합니다. 한 유명한 아이덴티티는 이렇게 말합니다.

exp(i ψ) = cos(ψ)+ i sin(ψ) [오일러 항등식]

따라서 exp(i ψ)를 사용하여 코사인파와 사인파를 동시에 설명할 수 있습니다.

​

아래는 주파수 Ω의 회전점 z=exp(i Ωt)가 시간에 따라 실제 축에서 코사인 x=cos(Ωt)를 생성하는 방법의 예입니다(gif 값이 움직이는 것으로 표시되는 경우).

이 지수 함수의 도함수는 i.exp(i ψ)이고 함수 자체를 다시 포함하므로 매우 편리합니다. 반면 코사인의 도함수는 사인으로 바뀌고 그 반대도 매우 짜증납니다.

문제는 실제 가치 양자 역학을 사용할 수 있는가 하는 것입니다.

​

Such a theory exists. We can split the wavefunction Ψ in two real valued wavefunctions, φ1 and φ2 as Ψ= φ1+i φ2 and also split the Schrödinger equation in two equations, containing both φ1 and φ2 in a coupled way. It works fine for simple calculations. The attitude of most scientists “why doing it in such a complex way using real wavefunctions, when complex functions are so much simpler… 😊

Yet the question came back every time again. The complication arises in calculations of entanglement. The real-valued-quantum-mechanics comes up with a different result in the calculation, meaning that the question can be tested experimentally. Is nature complex-valued or real-valued? After all, all observations are real-valued!

This year two independent studies demonstrate experimentally that a formulation of quantum mechanics involving complex rather than real numbers is necessary to reproduce experimental results.

Quantum mechanics now is officially complex!”

​

그러한 이론이 존재합니다. 파동함수 Ψ를 두 개의 실수 값 파동함수 ψ1 및 ψ2로 Ψ= ψ1+i ψ2로 분할할 수 있으며 슈뢰딩거 방정식을 결합 방식으로 ψ1과 ψ2를 모두 포함하는 두 방정식으로 분할할 수 있습니다. 간단한 계산에는 잘 작동합니다. 대부분의 과학자들의 태도는 “복잡한 함수가 훨씬 더 간단한데 왜 실제 파동함수를 사용하여 이렇게 복잡한 방식으로 수행하는가… 😊

​

그런데 그때마다 질문이 돌아왔다. 복잡함은 얽힘 계산에서 발생합니다. 실수치 양자역학은 계산에서 다른 결과를 도출하는데, 이는 문제를 실험적으로 테스트할 수 있음을 의미합니다. 자연은 복소 가치인가, 실재 가치인가? 결국, 모든 관찰은 실제 가치가 있습니다!

​

올해 두 개의 독립적인 연구는 실험 결과를 재현하기 위해 실수보다는 복소수를 포함하는 양자 역학의 공식화가 필요하다는 것을 실험적으로 입증했습니다.

이제 양자역학은 공식적으로 복잡해졌습니다!”