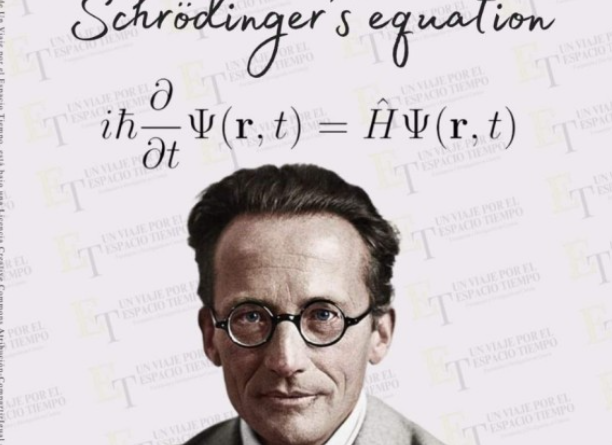슈뢰딩거 파동방정식 이해!
“Imagine that you have a piano keyboard, and each key corresponds to a possible location of a particle. The Schrodinger equation tells you how to play a melody on this keyboard, using the wave function as the sheet music.
The wave function gives you the amplitude and frequency of each note, which represent the probability and energy of finding the particle at that location. The higher the amplitude, the louder the note, and the higher the frequency, the higher the pitch.
v/@PhysInHistory
The Schrodinger equation also tells you how the melody changes over time, depending on the potential energy of the particle at each location. The potential energy is like a tuning knob that affects the frequency of each note.
If the potential energy is high, the note becomes sharper, and if it is low, it becomes flatter. The Schrodinger equation describes how the wave function evolves in response to these changes in frequency, and how the melody becomes more or less harmonious.
The equation is very important in quantum mechanics, because it allows us to calculate the wave function for any physical system, and use it to predict the outcomes of measurements.
However, unlike classical music, quantum music is very unpredictable and probabilistic. We can only know the average values of observable quantities, such as position and momentum, but not their exact values for any given measurement. Moreover, we can never know the wave function completely, because every time we measure it, we disturb it and change its shape. This is known as the collapse of the wave function, or the quantum jump.
It was discovered by Erwin Schrödinger in 1926, and it is based on the conservation of energy. It is a partial differential equation, which means that it involves derivatives of the wave function with respect to both space and time. It can be written in different forms depending on whether we use a fixed or a moving frame of reference. It can also be generalized to include relativistic effects, such as when particles move close to the speed of light.”
[https://tinyurl.com/mrxxuvhv](https://tinyurl.com/mrxxuvhv?fbclid=IwAR1QQu5Frn667fhbDPkXu39h5yntMD474OWD7NijhNS9BYqF3WhSk0AvJjs)
“피아노 키보드가 있고 각 건반이 입자의 가능한 위치에 해당한다고 상상해 보십시오. 슈뢰딩거 방정식은 파동 함수를 악보로 사용하여 이 키보드에서 멜로디를 연주하는 방법을 알려줍니다.
파동 함수는 각 음표의 진폭과 주파수를 제공하며, 이는 해당 위치에서 입자를 찾을 확률과 에너지를 나타냅니다. 진폭이 높을수록 음이 커지고, 주파수가 높을수록 음높이가 높아집니다.
v/@PhysInHistory
슈뢰딩거 방정식은 또한 각 위치에서 입자의 위치 에너지에 따라 시간이 지남에 따라 멜로디가 어떻게 변하는지 알려줍니다. 위치 에너지는 각 음표의 주파수에 영향을 미치는 조율 손잡이와 같습니다.
위치 에너지가 높으면 음표는 더 날카로워지고, 낮으면 납작해집니다. 슈뢰딩거 방정식은 이러한 주파수 변화에 반응하여 파동 함수가 어떻게 진화하는지, 그리고 멜로디가 어떻게 조화를 이루는지 설명합니다.
방정식은 모든 물리적 시스템의 파동 함수를 계산하고 이를 사용하여 측정 결과를 예측할 수 있기 때문에 양자 역학에서 매우 중요합니다.
그러나 클래식 음악과 달리 양자 음악은 매우 예측 불가능하고 확률적이다. 위치, 운동량 등 관측 가능한 양의 평균값만 알 수 있지만 특정 측정에 대한 정확한 값은 알 수 없습니다. 더욱이 파동함수를 완전히 알 수는 없습니다. 파동함수를 측정할 때마다 파동함수를 교란시키고 모양을 바꾸기 때문입니다. 이것을 파동함수의 붕괴, 즉 양자도약이라고 합니다.
1926년 에르빈 슈뢰딩거(Erwin Schrödinger)가 발견했으며 에너지 보존에 기초를 두고 있습니다. 이는 편미분 방정식으로, 이는 공간과 시간 모두에 대한 파동 함수의 미분을 포함함을 의미합니다. 고정된 기준틀을 사용하는지, 움직이는 기준틀을 사용하는지에 따라 다양한 형태로 기록될 수 있습니다. 또한 입자가 빛의 속도에 가깝게 움직일 때와 같은 상대론적 효과를 포함하도록 일반화할 수도 있습니다.”